以数织图

在以数织图游戏里，玩家可挑战大量数字关卡。于关卡中，玩家得通过填格子完成挑战。随着关卡逐步推进，提示会愈发复杂，玩家需动动脑筋，才能顺利解出格子中的图形。游戏会为玩家提供诸多提示，玩家能借助这些提示找到解法，助力顺利通关。

游戏背景：

以数织图拥有海量的关卡内容。在游戏里，玩家需采用填格的方式绘制图形。这里存在众多关卡，每个关卡填格子的顺序皆不一样。玩家得留意两边的数字提示，以此找出填格顺序，从而顺利画出关卡对应的图像。

游戏特色

1. 纵横数字游戏与文字游戏都极为实用，你对此相当熟悉，其游戏玩法更是让人极易上瘾。

2. 众多不同主题的拼图正等您来挑战，可别忘记领取成就奖励哦。

3、设有5种挑战模式，您可从中挑选最适宜自己的数织游戏难度等级。

4、舒缓愉悦的背景音乐，可让人迅速放松身心。

以数织图游戏攻略

本系列里的简称及其阐释

1、排：行/列

2、垂直：方向与排的走向呈垂直状态。

3、自k排起的m×n区块：当未特别指明时，一般指游戏里所有排构成的集合。它也能够用来表示一个矩形范围，在此范围内，m代表行，n代表列。

4、场地格：处于初始状态的格子，存在于游戏的区块之中。

5、第x行格：从任意一侧起计数的第x个场地格

6、第x个数字：从任一侧起计数的第x个数字

7、数字x的正格：此格必定存在黑块，并且该场地格必然是数字x所对应图形的组成部分。

8、负格：绝对不存在黑块的格子

9、数字x的位：指数字x有可能代表的场地格

第一章：数字数位的明确化

1-1概述

在数织时，我们面对的是一些位置模糊的情况，借助这些模糊位置与区块之间的相互关系，能够确定其中一部分的准确位置，最终成功推理出完整的图像。

数字的精确位置，通常可依据一排的格数与数字推导得出，偶尔也会用到已确定的正格和负格，仅有极少数关卡需同时借助两排以上的信息。正因如此，它的难度并非特别高。本系列旨在助力您从初出茅庐的新手，快速成长为能够推理大多数图形的高手。

注意：在以下所有的定理与方法里，我们会把负数视作零。

1-2 推演基础

要怎样才能借助推演来确定精准位置呢？不妨先提出一条极为简单的定理。

若一排仅有一个数字，那么除该数字所在位之外，其余场地格均为负格。(1 - 2 - 1)

这条定理无需证明便显而易见，从某种角度而言，它是数字位定义的另一种表述方式。

从这条公理能够知晓，要明确一个数字的精确位置，需将其位数削减至不能再减的程度。而交叉排列与单排的限制条件，有助于我们降低数字的位数。

下面来看一个简单的例子。

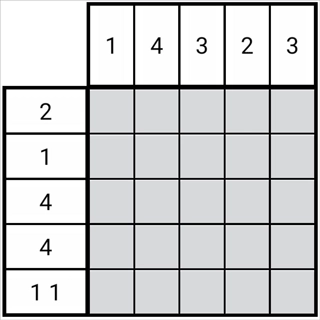
图1-2-1

如图可见，每一排黑块依据规则，均存在有限种分布情形，这些分布情形被称作分布可能。

从图里能发现，第二列存在两种分布的可能性。并且这两种分布可能性之间存在一些公共区域，很明显，该公共区域里的格子必定是正格。

同样地，在图中的第三列，存在三种分布的可能性。而在这三种分布可能性里，有一个公共部分，也就是第三列的第三格。所以，这个格子必然也是正格。

更普遍来说，在一排所有可能的分布情形里，始终存在黑块的格子属于正格。

若一个排仅有一个正格且该正格内只有一个数字，我们可将其视作“固定”此数字所在位的“钉子”。在位的左右两侧，能够“波动”，即增加格数，如此便可得出所有可能的分布情况。

与此同时，若有两个正格限定了一个数字的位置，那么这两个正格中间的部分必然也为正格。我们还能用数学语言将其表述为：

若一排仅有一个数字，且第m行格与第n行格都确定为正格，那么第i行格为正格。这里，i属于集合{x属于正整数|m≤x≤n或者n≤x≤m}。(1 - 2 - 2)

然而，鉴于数字间大小存在特定关系，一个数字的位会在正格的两侧增添一定数量的格数。但增添的格数不能超出数字所规定的范围，接下来我们从数学角度对这一情况展开推导。

假设在一排中仅有一个数字k，第m行格和第n行格是已知的正格，并且m≥n 。依据式1 - 2 - 2 ，可以知道这两行中间的所有格都是正格，一共占据了(m - n + 1)格。那么，位于左右两边能够增加的格数就是k - (m - n + 1) 。因此，从两端增加这么多格数就能得到所有的位置。也就是说，从第n - [k - (m - n + 1)]行格到第m + [k - (m - n + 1)]行格都属于该数字的位置。整理之后可以得出：

若某一排仅有一个数字k，同时第m行格与第n行格均为正格（m≧n），那么该数字的位置范围是从第(-k + m + 1)行格到第(k + n - 1)行格 。(1 - 2 - 2)

1-3边缘法

前文提到数字能够限制位，实际上，还有另一种事物也能起到限制位的作用，那便是场地格的边缘。很明显，场地格边缘以外不可能存在位，特别是第一个数字，它必定是离场地格边缘最近的，因而极易受到限制。基于此，我们很有必要探讨一下边缘的相关情况。

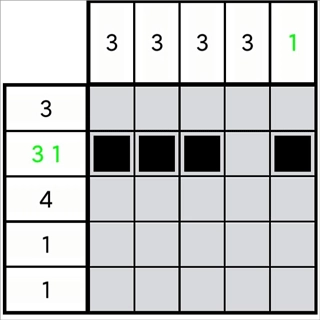
图1-3-1

从图1-3-1中能够明显看出，图里第1列的位无法向上增加两格，可它确实是满足定理(1-2-3)的前置条件的。我们不妨换个思路来考虑，要是不能向上增加，那就必然要向下增加。所以，向上无法增加的格数，就是向下需要增加的格数。

假设在某一排中，存在且仅存在一个数字m ，同时已知第n行的格子是正格，并且满足m > n 。那么，这一排无法增加的格数为(m - n)格。若将这些格数向下增加，那么可以得出：

若某一排仅有一个数字m，并且第n行格是正格，同时满足m>n，那么对于i∈[n，m]且i∈N+ ，第i行格均为正格。(1 - 3 - 1)

观察此定理，当m>n时，这意味着该数字所代表的位必定覆盖了第1行格至第n行格。倘若我们假定它是第一个数字，那么不难想到，这个定理依旧成立。于是可得：

若某一排中第n行的格是正格，并且这一格的第一个数字为m ，那么满足i∈[n，m]且i∈N + 的第i行格均为正格 。（需满足m > n ）(1 - 3 - 2)

当某个数字处于边缘位置时，它的状态并没有太大改变。然而，要是我们探讨一整排的情形，那又会怎样呢？

在此，我们引入一种方法——整体法。当明确两个相邻数字的数位时，可将这两个数字视作一个数字来处理，它们的数位就当作这个新数字的数位。这种处理方式能够简化运算，还有助于我们对一整排的情况进行分析。

我们能够留意到这样一个事实：当由多个数字构成的整体处于边缘位置时，会呈现出一种独特的分布形式——数字 - 空格 - 数字 - 空格。这种分布方式将数字所占据的空间压缩到了最小程度，我们把这种整体处于边缘的分布状况称作边缘状态。

假设存在一个实心物体在一条直道中进行滑动，不难想象，随着滑动的进行，该物体此时的投影与初始时刻投影的公共部分的大小会持续减小。所以，在物体所有运动瞬间投影的公共部分，实际上和其处于边缘状态时投影的公共部分是一样的。基于此，我们能够得出：

一排中不存在负格时，所有可能分布情况的公共部分是由其边缘状态所决定的。

不难发现，这种描述表面上近乎完美，实则存在一处细微瑕疵。具体而言，从整体角度看，多个数字所占空间能够伸缩变化，且处于边缘状态时必定是最短的。不过，的确，我们距离将其完善仅有一步之遥。

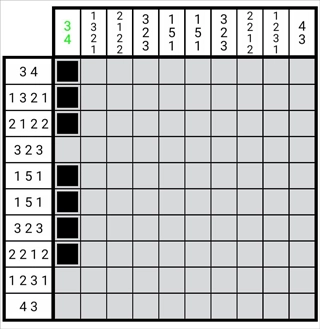
图1-3-2

如图所示，我们能够在第一列由上至下构建一个图形，该图形呈现的是第一列所有数字整体的边缘形态。此时，从这一列的底部往上数，会发现存在2个空格。这表明此图形中每个数字的位置都能够向下增添两格，所以我们把图形里对应每个数字的图形由上往下减少两格，即如图呈现的样子。

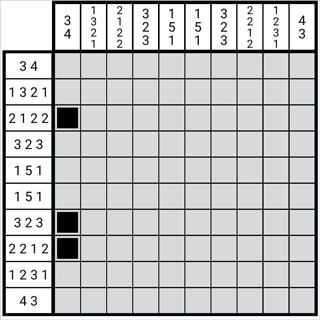
图1-3-3

如此，我们便获取了这一列的正格。通过这种方法得到的最终图形，与原来图形的数字位是相互对应的。在此，我们略去了对边缘状态的检查。边缘状态的重叠并非关键，关键在于重要数字与图形务必一一对应。由于这个图形能够变长或变短，然而其中任一图形的活动范围存在限制，该限制恰好是其自身与区块的长度。唯有当图形与数字一一对应时，这种方法才具备意义。基于此，我们反向推导出了其必然一一对应的原因，同时也能够将该性质应用于解题过程中。这同样是为第二章所做的一些铺垫。

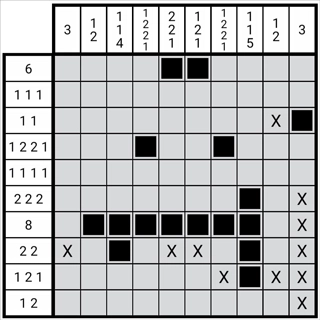
图1-3-4

如图所示，图中第七列第七行的数字2，是通过此方法确定的，为第七列第3个数字。基于位置关系的对应，第七列第4个数字1必然位于第七列第十行。

综上所述，我们能够归纳出一种快速确定正格的办法：首先，从第一行的格子起，按顺序在一排中做出如上述的数字 - 空格图形。接着，从起始方向减去最终剩余的空格数量，若得出负数则视作零。如此一来，最后所得到的图形必定是正格。而且，这些图形与原图形中的位置关系相互对应，它们也是运用第一章的所有方法所能获取的数量最多的正格。这种方法就叫做边缘法。

游戏亮点

1. 通过像素化逻辑谜题探寻更多线索，从而揭开隐匿其中的图像。

2. 纵横数字与文字游戏简单易上手，内容皆是你熟知的知识，玩法十分容易让人上瘾。

3、挑选最契合自身的难度，从初始状态逐步提升游戏难度。

小编点评：